MARCO TEORICO

Geometría plana

Proyecto final elaborado por estudiante de 5to de primaria  


La geometría plana es una parte de la geometría que trata de aquellos elementos cuyos puntos están contenidos en un plano. La geometría plana está considerada parte de la geometría euclídea, pues ésta estudia los elementos geométricos a partir de dos dimensiones.

PUNTO:
El punto es lo que no tiene ninguna parte. Es una figura geométrica sin dimensión, longitud, área, volumen. No es un objeto. Describe una posición en el espacio, determinada respecto de un sistema de coordinadas preestablecidas.



RECTA:

Una recta es una sucesión infinita de puntos, situados en una misma dirección.Una recta tiene una sola dimensión: la longitud.
Las lineas pueden ser abiertas, cerradas, horizontal, vertical, oblicua o diagonal.
Las rectas se nombran mediante dos de sus puntos o por una letra minúscula.Dos puntos determinan una recta.



Clases de recta

-Secantes

Las rectas secantes se cortan en un punto



-Paralelas

Las rectas paralelas no se cortan en ningún punto.



-Perpendiculares

Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales de 90º.



SEMIRRECTA

El concepto de semirrecta se utiliza en geometría para identificar a cada uno de los fragmentos en que toda recta puede ser dividida por cualquiera de los puntos que la componen. Es importante tener en cuenta que la forma correcta de escribir esta palabra es con dos ‘r’ y no semirrecta (con una sola R).

La semirrecta, por lo tanto, puede presentarse como la porción de una línea recta que está compuesta por todos los puntos que se localizan hacia uno de los costados de un determinado punto fijo que se toma como referencia: esto quiere decir que una semirrecta tiene un origen (el punto que le da inicio) pero se extiende hacia el infinito. La recta, en cambio, no tiene ni comienzo ni final.



SEGMENTO

Parte de una recta que tiene dos puntos extremos. Se nombra con letras mayúsculas, que señalan el punto de inicio y el final del segmento.



SIMETRÍA

Una figura es simetrica cuando al doblar sus dos mitades coinciden exactamente, la linea del dobles se denomina eje de simetría



ÁNGULO

Se forma con la unión de dos semirrectas o lados que tienen un origen común o vértice.



VÉRTICE

En geometría, vértice es el punto donde se encuentran dos o más semirrectas que conforman un ángulo.



MEDICIÓN DE ÁNGULOS

Para medir la amplitud de un ángulo se usa el transportador
-Coloca el transportador de tal manera que su centro coincide con el vértice del ángulo y uno de sus lados pase por 0°
-Observa en el transportador el número por el que pasa el otro lado del ángulo. Este número corresponde a su medida en grados.



CLASES DE ÁNGULOS

Según la inclinación de las rectas, el ángulo será más abierto o más cerrado. El valor de los ángulos se mide en grados.



ÁNGULO AGUDO

Es el ángulo más cerrado, que tiene siempre menos de 90 grados.



ÁNGULO RECTO

Es el que tiene un valor invariable de 90 grados.



ÁNGULO OBTUSO

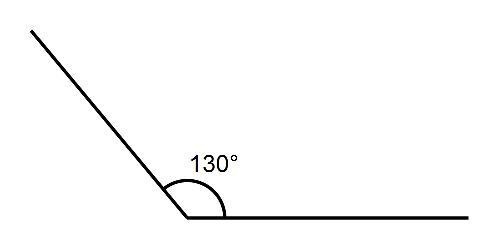
Es el que tiene una abertura mayor de 90 grados, pero menor de 180 grados.



ÁNGULO LLANO

Es el que mide 180 grados.



ÁNGULO CÓNCAVO

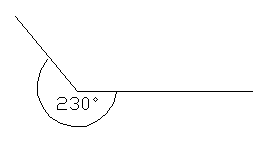
Son los ángulos que van de 180° a 360°



ÁNGULO CONVEXO

Son los ángulos que van de 0° a 180º



ÁNGULO COMPLETO

Es el angulo que le da toda la vuelta al circulo. Angulo completamente cerrado.



ÁNGULO NULO

Es el que no tiene amplitud y mide 0°.



ÁNGULOS COMPLEMENTARIOS

Dos ángulos son complementarios cuando sus medidas suman 90°



ÁNGULOS SUPLEMENTARIOS

Dos ángulos son suplementarios cuando sus medidas suman 180°.



CONSTRUCCIÓN DE ÁNGULOS

Para construir un ángulo debe seguir los siguientes pasos:



POLÍGONOS

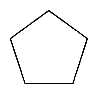
Son figuras cerradas, formadas por varios segmentos y pueden ser regulares e irregulares.



POLÍGONOS REGULARES

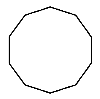
Sí todos sus lados tienen la misma longitud y todos sus ángulos son iguales.



POLÍGONOS IRREGULARES

Son los que tienen sus lados con diferente longitud y sus ángulos son de diferente medida.



TRIÁNGULO

Es una figura geométrica que tiene tres lados y tres vértices.



CLASES DE TRIANGULO SEGÚN SUS LADOS:




-TRIANGULO EQUILATERO:

Tiene los tres lados de igual Longitud.



-TRIANGULO ISOSCELES

Tiene dos lados de igual longitud.



-TRIANGULO ESCALENO

Tiene tres lados de diferente longitud.



CLASES DE TRIÁNGULO SEGÚN SUS ÁNGULOS:

-Rectángulo: Tiene un ángulo recto


-Acutángulo: Tiene 3 ángulos agudos


-Obtusángulo: Tiene un ángulo obtuso



RECTÁNGULO

Es un cuadrilátero que tiene los lados opuestos, paralelos, y sus lados contiguos perpendiculares.



CUADRADO

Es un cuadrilátero que tiene todos lados de igual longitud. Cada uno de sus ángulos internos mide un cuarto de vuelta.

 


CLASIFICACIÓN DE LOS CUADRILÁTEROS Y PARALELOGRAMOS




ROMBO

El rombo es un cuadrilátero paralelogramo cuyos cuatro lados son de igual longitud



ROMBOIDE

Se denomina romboide al paralelogramo que no es ni rombo ni rectángulo, es decir, un paralelogramo que tiene sus ángulos y sus lados iguales dos a dos . Comúnmente se lo llama paralelogramo o también paralelogramo no rectangular.



PARALELOGRAMO

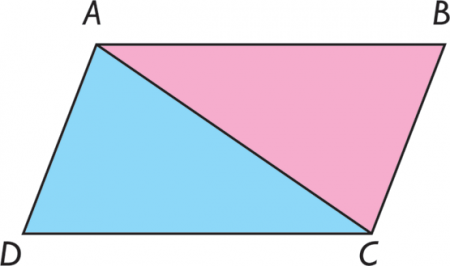
Un paralelogramo es un tipo especial de cuadrilátero (un polígono formado por cuatro lados) cuyos lados son paralelos dos a dos.



TRAPECIO

En geometría, se llama trapecio a un cuadrilátero que tiene dos lados paralelos y otros dos que no lo son. Los lados paralelos se llaman bases del trapecio y la distancia entre ellos altura



SEMEJANZAS Y DIFERENCIAS DE LOS PARALELOGRAMOS

PARALELOGRAMO	SEMEJANZAS	DIFERENCIAS
Un cuadrado y un rombo	Ambos tienen los cuatro lados iguales	El cuadrado tiene sus cuatro lados iguales y el rectángulo no
Un cuadrado y un rectángulo	Ambos tienen cuatro ángulos rectos	El cuadrado tiene sus cuatro lados iguales y el rectángulo no
Un romboide y un rombo	Ambos tienen sus ángulos opuestos iguales	El rombo tiene sus cuatro lados iguales y el romboide no

CIRCUNFERENCIA

La circunferencia es una línea curva y cerrada donde todos sus puntos están a igual distancia del centro.



CÍRCULO

Es la región del plano delimitada por una circunferencia y que posee un área definida



FIGURAS BIDIMENSIONALES

Algo es bidimensional si tiene dos dimensiones, por ejemplo, ancho y largo, pero no profundidad. Los planos son bidimensionales, y sólo pueden contener cuerpos unidimensionales o bidimensionales.



OBJETOS TRIDIMENSIONALES

En geometría y análisis matemático, un objeto o ente es tridimensional si tiene tres dimensiones. Es decir cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Por ejemplo, anchura, longitud y profundidad.



CUERPOS

Todos los objetos que hay a nuestro alrededor se denominan cuerpos.



SÓLIDOS

Sólidos o poliedros son cuerpos simétricos cuyas caras son polígonos que tienen aristas y vértices.



EL CUBO

Un cubo o hexaedro regular es un poliedro de seis caras cuadradas congruentes. Todas sus caras son de cuatro lados y paralelas dos a dos



PRISMA

Un prisma es un poliedro que tienen dos caras paralelas e iguales llamadas bases y sus caras laterales son paralelogramos



ESFERA

Un objeto tridimensional con la forma de una pelota. Todos los puntos de su superficie están a la misma distancia del centro.



CILINDRO

Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados



PIRÁMIDE

Es un poliedro limitado por una base, que es un polígono con una cara; y por caras, que son triángulos coincidentes en un punto denominado ápice



PERÍMETRO

Es calcular la medida del contorno de cada figura, para lo cual se usa las medidas de sus lados y se suman.



ÁREA

Es la medida de la superficie, que se expresa en unidades cuadradas, y se hayan multiplicando un lado por la altura.
La unidad básica de medida de àrea es el metro cuadrado, que corresponde a una superficie cuadrada de un metro de lado.



PLANO CARTESIANO

El plano cartesiano es un sistema de coordenas, representado por dos rectas numéricas perpendiculares, cuyo punto común es el cero.
La recta Horizontal recibe el nombre de eje de las abscisas y la vertical se denomina eje de las ordenadas.



PAREJA ORDENADA

Una pareja ordenada esta formada por dos coordenadas, que indica la posición de un plano cartesiano.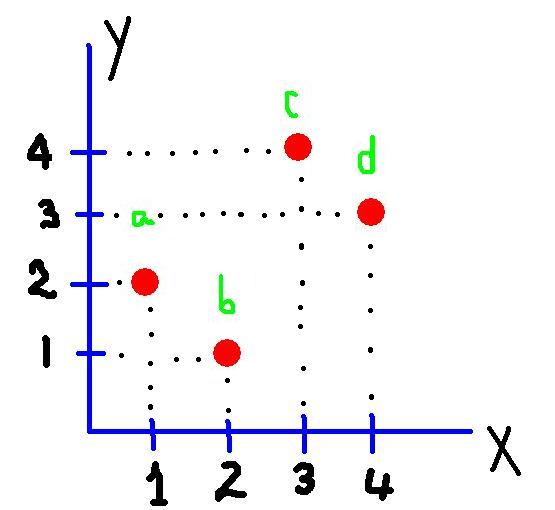



MOVIMIENTOS EN EL PLANO

Traslación cuando se desliza una figura a lo largo de una recta, sin cambiar su forma ni su tamaño, la nueva figura recibe el nombre de traslación.
Rotación cuando se gira una figura al rededor de un punto, llamado centro de rotación se obtiene una nueva figura denominada imagen de rotación.

Por la rotación es necesario conocer el ángulo de giro: Es positivo si se da en sentido contrario al movimiento de las manecillas del reloj, y negativo si se da en el mismo sentido de las manecillas.